Deep Learning con TypeScript

El campo de la Inteligencia Artificial comenzó a desarrollarse después de la Segunda Guerra Mundial (el nombre se acuñó en 1956). Pero no fue hasta finales del S. XX cuando empezaron a verse las aplicaciones de uso masivo, con los primeros detectores de SPAM o los motores de recomendación.

En los años 20 del S. XXI la aparición de las Inteligencias Artificiales Generativas parece a punto de revolucionar la manera en que las personas se relacionan con la tecnología.

Para usuarios finales, permite poder “hablar con Internet” y hacer preguntas o solicitar servicios a sistemas que entienden el lenguaje natural y, lo más importante, responden de igual manera.

Para los profesionales la posibilidad de que una IA asuma una parte de las labores, incluso algunas de las más “creativas” supone un cambio de paradigma cuyas consecuencias tardaremos décadas en comprender del todo.

Y para nosotros, los que hacemos software, el campo de la IA representa simplemente el futuro. Es muy poco probable que un programador que empiece su carrera profesional en 2030 no tenga que trabajar a diario usando Inteligencia Artificial, para escribir código, para evaluarlo o para requerir servicios de terceros.

Por eso considero vital para cualquier programador tener al menos una noción general de cómo funciona una Inteligencia Artificial, de la misma forma que hay que tener conocimientos de algoritmia básica.

Y un concepto central en la IA es el de las Redes Neuronales Artificiales y el Deep Learning.

En este artículo voy a intentar explicar todo lo necesario para entender cómo funciona el Deep Learning y programar tu propia Red Neuronal.

El código de ejemplo está escrito con TypeScript porque es un lenguaje fácil de entender y se puede programar incluso dentro del mismo navegador web. Aunque en la vida real nunca usarías este lenguaje para desarrollar un modelo y ponerlo en producción debido al pobre rendimiento, lo importante para aprender es usar un lenguaje en el que programes con comodidad.

Puedes encontrar el código fuente de este artículo en este repositorio de GitHub.

Ten en cuenta que para programar una Red Neuronal Artificial es necesario entender no sólo cómo funciona la propia red, sino el proceso de entrenamiento.

Como vamos a ver, lo primero es relativamente sencillo. Pero para entender cómo funciona el proceso de entrenamiento necesitarás algunos conocimientos de cálculo. En particular, necesitarás cierta soltura con:

• Funciones lineales
• Derivación y gradiente
• Vectores y Matrices

Pero tampoco te asustes, con que entiendas a nivel general los conceptos es suficiente, no hay que ser matemático profesional ni mucho menos.

Disclaimer

La red que vamos a estudiar es una maqueta, un juguete. No me dedico a programar este tipo de modelos profesionalmente, así que seguro que muchas de las decisiones que he tomado no son las óptimas.

Mi objetivo es que, si sigues este artículo y usas mi código como ejemplo para construir tu propio modelo aprendas todo lo posible sobre el funcionamiento de las redes neuronales. Yo mismo he hecho eso con este otro artículo de Douglas Reiser, pero no es más que eso: un ejercicio para aprender.

Tómatelo como un pequeño barco de entrenamiento en el que los niños aprenden a navegar a vela: funciona en lo esencial, pero no lo usarías para cruzar el pacífico ;-)

Vale, al lío.

1. ¿Qué es Deep Learning?

Antes de entrar en materia, es importante que demos algo de contexto para entender dónde estamos exactamente. Empecemos por el principio:

La Inteligencia Artificial (IA) es una rama de las ciencias de la computación que busca desarrollar agentes que simulen el razonamiento humano.

El Machine Learning (ML) es una rama de la IA que busca generar software capaz de entrenar un modelo de la realidad a partir de datos conocidos, para buscar patrones y hacer predicciones.

Hay dos tipos principales de Machine Learning:

• ML supervisado, en el que los datos de entrenamiento vienen etiquetados. Por ejemplo, cuando en Google Photos identificas la cara de tus familiares para que agrupe todas las fotos en las que sale una misma persona, estás participando en el aprendizaje supervisado de un modelo de ML.
• ML no supervisado, en el que se trabaja con datos sin etiquetar para buscar patrones o grupos naturales. Por ejemplo, cuando Netflix te propone series “basadas en tus preferencias”, está usando un modelo de aprendizaje no supervisado en el que te ha metido en un grupo con otros usuarios que ven contenido similar al que ves tu, y te recomienda lo que les haya gustado a ellos.

El Deep Learning es una rama del Machine Learning, en el que se usa un tipo de modelos llamado “Redes Neuronales Artificiales”. La principal ventaja de estos modelos respecto a otros tipos de ML es que pueden identificar (aprender) patrones más complejos.

Las “Inteligencias Artificiales Generativas” como Dall-E y los “Large Language Models” (LLMs) como ChatGPT o Google Bard son una ramas del Deep Learning.

En este artículo nos centraremos en entender cómo funcionan las redes neuronales, el Machine Learning Supervisado, y sobre todo, cómo programar una Red Neuronal desde cero con TypeScript.

2. ¿Cómo funciona una Red Neuronal Artificial?

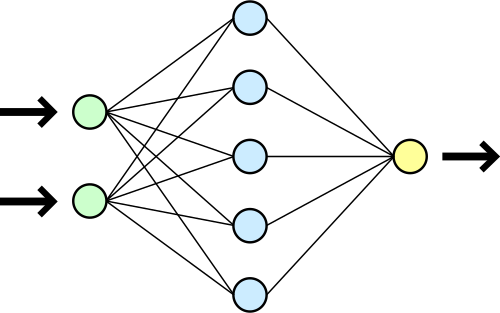
La idea detrás de las redes neuronales es muy simple. Son estructuras formadas por nodos organizados en capas. El funcionamiento a grandes rasgos es:

1. Cada nodo ejecuta una función matemática que llamamos “función de activación”, y que para una determinada entrada nos devuelve una determinada salida.
2. La primera capa recibe los valores de entrada, uno por cada nodo, y cada nodo calcula su valor de salida.
3. En cada nodo de la segunda capa, la entrada es suma ponderada de las salidas de los nodos de la capa anterior (o sea, cada salida de un nodo se multiplica por un peso, y se suman todos los valores), más un valor adicional llamado “sesgo”.
4. Este proceso se repite capa por capa hasta que se tiene la salida de la red, que es el resultado de los nodos que componen la última capa.

En lenguaje matemático:

Para cada nodo de una capa particular definimos

\begin{equation} a = f(z), \end{equation}

\begin{equation} z = w_0a_0 + w_1a_1 + \cdots + w_na_n + b \end{equation}

donde

• \(a\) es el resultado de la función de activación
• \(z\) es la suma de las activaciones de los nodos de la capa anterior \(a_i\) multiplicadas por sus pesos \(w_i\), más un sesgo \(b\).

¿Qué es la Función de activación?

Una de las cosas que hay que enteder con las redes neuronales, y con el aprendizaje automático en general, es que los conceptos son sencillos, pero hay una gran cantidad de decisiones que no tienen una explicación científica que las justifique.

La función de activación es un ejemplo de esto. En principio, casi cualquier función nos vale, pero dependiendo de para qué vayamos a usar la red neuronal, unas funcionan mejor que otras.

Es habitual que la función de activación sea diferente en la capa de entrada, en las capas ocultas y en la capa de salida. Por simplicidad, usaremos una única función de activación de momento.

Una de las elecciones más frecuentes es usar una función sigmoide, por ejemplo la curva logística:

\begin{equation} f(z) = {1 \over (1 + e^{-z})} \end{equation}

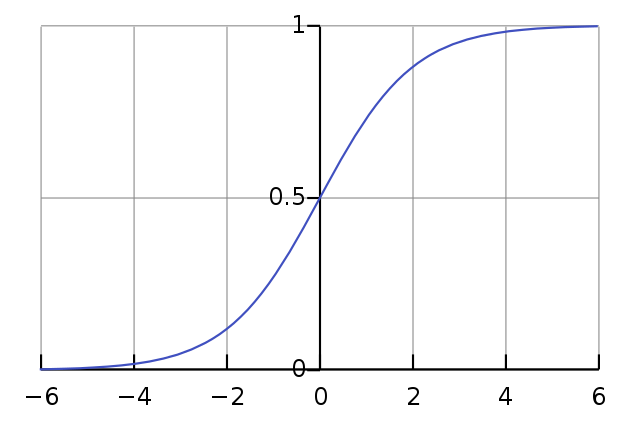Fuente: Wikipedia

Se trata de una función que siempre dará un valor entre 0 y 1 para cualquier valor de \(z\). Además es una función continua y derivable, lo que es útil para el entrenamiento como veremos más adelante.

¿Y el Sesgo?

El valor \(b\) de sesgo que vimos en el apartado anterior está para añadir un umbral a la suma ponderada.

Podemos entenderlo como el valor que tiene que superar la suma para que \(z\) sea positivo, y por tanto la función de activación pase de valores cercanos a 0 a valores cercanos a 1.

3. Código de la red neuronal

La red neuronal está representada por las clases Network y Node:

export default class Network {

    private _input: number[] = [];

    constructor(
        readonly layers: Node[][],
        readonly activationFunction: ActivationFunction) { }

 ... 

    public calculate(input: number[]): number[] {
        this._input = Object.assign([], input);

        if (input.length !== this.layers[0].length) {
            throw (`Input size (${input.length}) doesn't match first layer size (${this.layers[0].length})`);
        }
        for (let layer of this.layers) {
            input = this.calculateLayer(input, layer);
        }

        this._output = input;
        return this._output;
    }

    private calculateLayer(input: number[], layer: Node[]): number[] {
        let result = []
        for (let node of layer) {
            result.push(node.calculate(input));
        }
        return result;
    }

    ...

export default class Node {
    private _zValue: number = 0;
    private _activation: number = 0;

...    
    calculate(input: number[]): number {
        this._zValue = this.calculateZValue(input);
        this._activation = this.activationFunction.calculate(this._zValue);
        return this._activation;
    }

    private calculateZValue(input: number[]): number {
        let sum = -1 * this.bias
        for (let i = 0; i < input.length; i++) {
            sum += this.weights[i] * input[i];
        }
        return sum;
    }
...

En esencia la clase Network tiene una matriz de dos dimensiones de nodos y una función de activación.

Cuando queremos calcular la salida de la red, iteramos sobre las capas y para cada capa iteramos sobre los nodos, pidiendo a cada nodo que calcule su valor de \(z\) y su valor de activación \(a\).

La salida de la red es un vector del tamaño de la última capa con las activaciones de sus nodos.

Para representar la función de activación programamos una clase abstracta que nos permita usar distintas implementaciones si queremos:

export default abstract class ActivationFunction {
    abstract calculate(input: number): number;

    abstract calculateFirstDerivative(input: number): number;
}

Como vemos, una función de activación tiene que ser capaz de darnos tanto el valor para una entrada, como la primera derivada. Veremos por qué cuando hablemos del entrenamiento.

La función de activación que usaremos será un sigmoide:

\begin{equation} f(z) = {1 \over (1 + e^{-z})} \end{equation}

\begin{equation} f’(z) = f(z)(1 - f(z)) \end{equation}

export default class SigmoidActivationFunction extends ActivationFunction {

    calculate(input: number): number {
        var output = (1 / (1 + Math.pow(Math.E, (-1) * input)));
        return output;
    }

    calculateFirstDerivative(input: number): number {
        const result = this.calculate(input);
        return result * (1 - result);
    }
}

La red neuronal se crea inicialmente con pesos y sesgos aleatorios, usando un Builder que nos permite establecer algunas de sus características:

const network = Network.builder([2, 5, 2]) // tres capas de 2, 5 y 2 nodos cada una
    .withWeightLimits(-1, 1) // con pesos aleatorios inicializados entre -1 y 1 (opcional)
    .withBiasLimits(-1, 1) // con sesgos aleatorios inicializados entre -1 y 1 (opcional)
    .withOutputProcessor(new NoOpFormatter()) // sin procesador de salida (opcional)
    .withActivationFunction(new SigmoidActivationFunction()) // con un sigmoide como función de actvación (opcional)
    .build();

Sobre el procesador de salida hablaremos más adelante.

4. ¿Cómo se entrena una red neuronal?

¿Cómo aprende un niño a distinguir una vaca de un caballo? Un niño no aprende a distinguir cada característica de cada animal para hacer una comparación en tiempo real entre ambos. Simplemente aprende porque desde puequeño las personas a su alrededor le van indicando “eso es un caballo”, “eso es una vaca”.

Pues una red neuronal aprende de la misma manera: le proporcionamos ejemplos una y otra vez para que vaya ajustando su estructura interna y sea capaz de reproducirlos.

Lo primero que necesitamos para enseñar a una red neuronal es una forma de medir su error, para poder buscar la manera de reducirlo. A la función que nos da el tamaño del error en una predicción de la red neuronal la llamamos función de coste.

Igual que con la función de activación, podemos elegir entre distintas opciones a la hora de seleccionar una función de coste. Una de las más habituales es el error cuadrático:

\begin{equation} C(a) = {1 \over 2 }(a - o)^2 \end{equation}

Donde \(a\) es la salida de la red neuronal y \(o\) es el valor esperado. Elevamos la resta \((a - o)\) al cuadrado para que siempre nos de valores positivos, y lo multiplicamos por \( 1 \over 2 \) para que al derivar nos quede simplemente:

\begin{equation} C’(a) = a - o \end{equation}

Una vez que tenemos una forma de calcular el error que ha cometido la red en una predicción, necesitamos un algoritmo para que la red pueda ajustar sus pesos y sesgos de manera que ese error se haga lo más pequeño posible.

Y para llevar esto al código necesitamos hablar de dos algoritmos: Descenso del gradiente y BackPropagation

¿Qué es el Descenso del Gradiente?

El algoritmo del descenso del gradiente se utiliza para encontrar el mínimo de una función, en nuestro caso, la función de coste.

La idea es la siguiente:

1. Partimos de una red neuronal inicializada con pesos aleatorios. Normalmente los sesgos se inicializan a cero.
2. Introducimos un conjunto de ejemplos de los que sabemos previamente el resultado esperado.
3. Pedimos a la red que calcule la salida para cada valor de entrada.
4. Calculamos el valor de la función de coste para cada resultado obtenido.
5. Calculamos el gradiente de la función de coste, que es la derivada multivariable de la función respecto a todos los parámetros de la red (los pesos y sesgos).
6. Modificamos cada peso sumándole un valor igual a la derivada de la función de coste respecto a ese peso en particular, con signo contrario, multiplicada por un valor que llamamos “tasa de aprendizaje” y que veremos más adelante. Hacemos lo mismo con los sesgos.
7. Repetimos los pasos 1 a 6 hasta que la función de coste ya no disminuya más.

¿Por qué? Veamos la justificación del algoritmo con detenimiento.

Como recordarás de cuando estudiaste cálculo, la derivada de una función (o el gradiente si hablamos de un campo vectorial) nos da la pendiente de la función. Si en un punto concreto la función sube con fuerza, la derivada evaluada en ese punto tendrá un valor positivo grande. Si por el contrario desciende, el valor será negativo. Y si la función es plana en ese punto, la derivada valdrá cero.

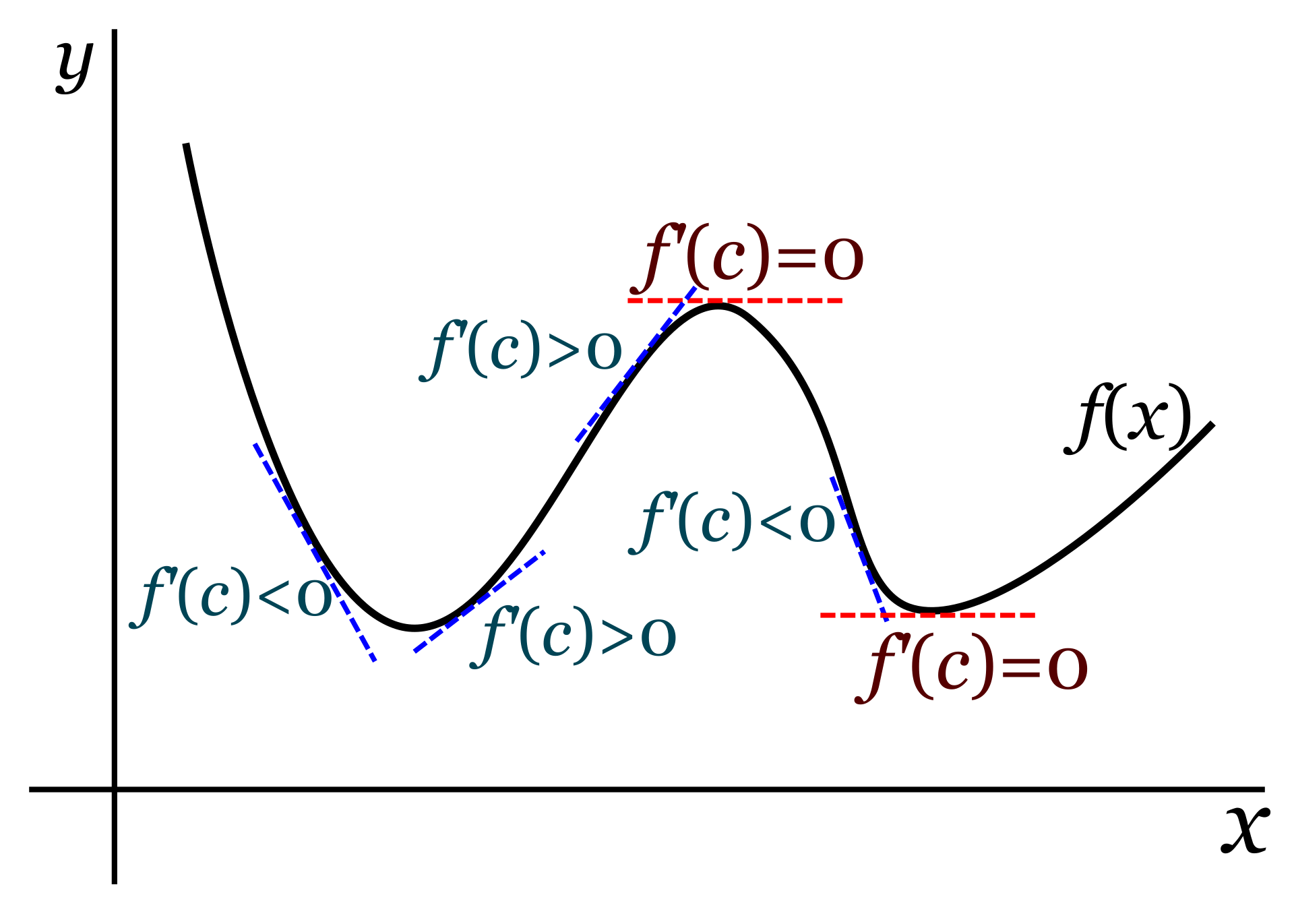Fuente: Wikipedia

Por tanto, identificamos un mínimo de la función como un punto para el que la derivada es negativa antes de ese punto, vale cero justo en el punto, y es positiva justo después.

La idea es que, si para un valor determinado del peso \(w_i\) la derivada de la función de coste respecto a ese peso es negativa, quiere decir que la función está descendiendo en ese punto. Como queremos andar hacia el mínimo de la función, deberemos probar con un valor más grande. Sin embargo, si la derivada es positiva, significa que la función está creciendo y lo que necesitamos es retroceder a un valor más pequeño de \(w_i\).

La tasa de aprendizaje vendría a ser el tamaño del salto que queremos dar al elegir el siguiente valor de \(w_i\). Por eso debemos elegirla con cuidado: si es demasiado grande, puede que nos saltemos un mínimo de la función. Pero si la elegimos demasiado pequeña, puede que el aprendizaje se estanque y no lleguemos nunca al mínimo.

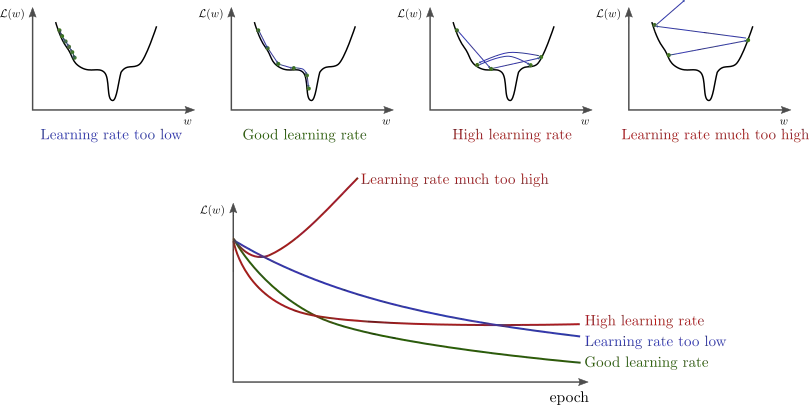Fuente: http://www.bdhammel.com/learning-rates/

Por tanto, para entrenar una red neuronal “sólo” necesitamos calcular la función de coste, y su derivada respecto a los pesos y sesgos, e ir probando valores hasta encontrar el mínimo.

Recuerda que, para un nodo de una capa en particular, el coste \(C(a)\) es una función de su activación, pero la activación es una función de su valor de z, y su valor de z es función de los pesos, los sesgos y las activaciones de los nodos de la capa anterior.

Llamemos \(C_0\) al coste de la última capa (que mide el error de la red al predecir el resultado de una entrada de ejemplo). Si queremos calcular la derivada parcial de \(C_0\) respecto del peso \(ij\)-ésimo de la capa \(l\) necesitamos aplicar la regla de la cadena:

\begin{align} \frac{\partial{C_0}}{\partial {{w_i}_j}^l} = \frac{\partial{z_j^l}}{\partial {{w_i}_j}^l} \frac{\partial{a_j^l}}{\partial z_j^l} \frac{\partial{C_0}}{\partial a_j^l} \end{align}

Y haríamos un cálculo análogo para encontrar la componente correspondiente al sesgo \(b_i^l\).

Y aquí nos encontramos dos problemas:

• por un lado, \(a_j^l\) es en realidad \(a_j^l({{w_i}_j}^{l-1}, a_j^{l-1}, b_j^{l-1})\): depende de los pesos, sesgos y activaciones de la capa anterior.
• además, los pesos y sesgos pueden ser varias decenas, miles o millones de parámetros, dependiendo del tamaño de la red.

Así que calcular la derivada no es en absoluto un tema trivial. Afortunadamente, es un problema que está estudiado y se resuelve con el algoritmo BackPropagation.

¿Qué es BackPropagation?

El algoritmo BackPropagation permite calcular el gradiente de la función de coste de forma eficiente. Consiste en recorrer las capas de la red desde la última hacia atrás, y para cada capa ejecutar la siguiente rutina sobre todos los nodos:

1. Si estamos en la última capa, calculamos la derivada de la función de coste respecto a la activación \(\frac{\partial{C_0}}{\partial a_i}\), y almacenamos el resultado en memoria.
2. Calculamos \(\frac{\partial{C_0}}{\partial b_i} = \frac{\partial{C_0}}{\partial a_i} \frac{\partial{a_i}}{\partial z_i} \frac{\partial{z_i}}{\partial b_i} \), sabiendo que el \(\frac{\partial{z_i}}{\partial b_i} = 1 \).
3. Para cada peso \(w_i\) del nodo:
   • Calculamos \(\frac{\partial{z_i}}{\partial w_i} \)
   • Calculamos \(\frac{\partial{C_0}}{\partial w_i} = \frac{\partial{C_0}}{\partial a_i} \frac{\partial{a_i}}{\partial z_i} \frac{\partial{z_i}}{\partial w_i} \) reutilizando los valores que ya teníamos del paso 2.
   • Si no hemos llegado aún a la primera capa, almacenamos la parcial del coste respecto a la activación de la capa anterior \(a_i^l\): \(\frac{\partial{C_0}}{\partial {a_i}^l} = \frac{\partial{C_0}}{\partial a_i} \frac{\partial{a_i}}{\partial z_i} \frac{\partial{z_i}}{\partial a_i^l} \), donde \(\frac{\partial{z_i}}{\partial a_i^l}\) es simplemente el peso \(w_i\) de esa actividad de la capa anterior en este nodo. En la siguiente vuelta del bucle, recuperaremos este valor para construir la siguiente componente del gradiente.

Se puede comprobar matemáticamente que este algoritmo produce el mismo resultado que aplicar la regla de la cadena.

Venga, vamos a ver el código.

5. Código del proceso de aprendizaje supervisado

Igual que hicimos con la función de activación, para la función de coste crearemos una clase abstracta y una implementación por defecto:

export default abstract class CostFunction {
    abstract calculate(actualResult: number, expectedResult: number): number;
    abstract calculateFirstDerivative(actualResult: number, expectedResult: number): number;

    private getCostArray(actualResult: number[], expectedResult: number[]): number[] {
        let cost: number[] = [];
        for (let i = 0; i < actualResult.length; i++) {
            cost.push(this.calculate(actualResult[i], expectedResult[i]));
        }
        return cost;
    }

    getTotalCost(actualResult: number[], expectedResult: number[]) {
        let costArray = this.getCostArray(actualResult, expectedResult);
        return costArray.reduce((a, b) => a + b);
    }
}

export default class QuadraticCostfunction extends CostFunction {

    calculate(actualResult: number, expectedResult: number): number {
        return Math.pow(actualResult - expectedResult, 2) / 2;
    }

    calculateFirstDerivative(actualResult: number, expectedResult: number): number {
        return actualResult - expectedResult;
    }
}

El proceso de entrenamiento lo puedes ver por ejemplo en este script:

const rounder = new OutputRounder();
const network = Network.builder([2, 2])
    .withWeightLimits(-1, 1)
    .withBiasLimits(0, 0)
    .withOutputProcessor(rounder)
    .build();
const epochs = 1000;
const batches = 1;
const output = new CliOutput();
const cost = new QuadraticCostfunction();
const learningRate = new LearningRate(0, 1);
const trainDataset: TrainDataItem[] = [];

trainDataset.push(new TrainDataItem([1, 0], [0, 1]));
trainDataset.push(new TrainDataItem([0, 1], [1, 0]));

const trainConfig = TrainConfig
    .builder(network, trainDataset)
    .withLearningRate(learningRate)
    .withEpochs(epochs)
    .withBatchCount(batches)
    .withCostFunction(cost)
    .withOutput(output)
    .withGainThreshold(0)
    .build();

const trainer = new Trainer(trainConfig);

const result = trainer.execute();

Queremos entrenar la red para que nos invierta el orden de los valores de entrada: si le damos [1,0] nos devolverá [0,1] y viceversa.

Para ello partimos de una red inicial con sesgos y pesos aleatorios a la que añadimos un procesador de salida que redondea los valores: de esta manera nos aseguramos de que siempre tengamos ceros o unos enteros en la salida, y reducimos el número de pasadas necesarias en los datos de entrenamiento, porque en cuanto el valor encontrado por la red sea inferior a 0.5 se redondeará a 0, y para valores mayores será 1.

Después creamos un conjunto de datos de entrenamiento, con objetos de la clase TrainDataItem que guardan un valor de entrada y el valor de salida esperado.

Después definimos la configuración del entrenamiento usando el builder de la clase TrainConfig:

• El objeto LearningRate nos permite definir los incrementos de pesos y sesgos en cada bloque de entrenamiento.
• El número de épocas, o veces que vamos a recorrer los datos de prueba (“epochs”)
• El número de lotes en que queremos dividir los datos de prueba. Por cada lote haremos el cálculo del gradiente de la función de coste y modificaremos los pesos y sesgos de la red.
• El umbral de ganancia: cuando entre dos épocas la mejora (en valor absluto) del coste no supere este valor, detendremos el entrenamiento aunque aún no hayamos alcanzado el número de epochs.

Por último, pasamos la configuración de entrenamiento al Trainer para que ejecute el proceso de aprendizaje:

export default class Trainer {

    constructor(private config: TrainConfig) { }

    execute(): TrainResult {
        let t0 = Date.now();
        const result = new TrainResult();

        let lastCost = 0;
        for (let epoch = 0; epoch < this.config.epochs; epoch++) {

            const epochResult = this.executeEpoch(epoch);

            epochResult.calculateGain(lastCost);
            result.epochResults.push(epochResult);
            this.config.output.write(`Epoch #${epochResult.epochNumber} total cost: ${epochResult.cost} (${epochResult.costGainPercent}%)`);
            lastCost = epochResult.cost;

            if (Math.abs(epochResult.costGain) < this.config.gainThreshold) {
                this.config.output.write(`\nReached cost gain threshold. Interrupting.`);
                break;
            }
        }
        let t1 = Date.now();

        result.durationMs = t1 - t0;
        return result;
    }


    private executeEpoch(epoch: number): TrainEpochResult {
        let t0 = Date.now();
        const result = new TrainEpochResult(epoch);
        const batches = this.config.batches;
        for (let i = 0; i < batches.length; i++) {
            this.executeBatch(batches[i], result);
        }
        let t1 = Date.now();
        result.duration = t1 - t0;
        return result;
    }

    private executeBatch(items: TrainDataItem[], result: TrainEpochResult) {
        const network = this.config.network;
        const costFunction = this.config.costFunction;
        const tunner = new NetworkTunner(this.config.network, this.config.learningRate);
        for (let i = 0; i < items.length; i++) {
            const item = items[i];
            const output = network.calculate(item.input);
            const backProp = new BackPropagation(network, item.expectedOutput, costFunction);
            backProp.calculate(tunner);

            result.cost += backProp.totalCost;
        }
        tunner.apply(network);
    }

En cada lote se calculará la salida de la red para los elementos de entrenamiento incluidos, y se ejecutará el algoritmo BackPropagation para parametrizar el NetworkTunner que calculará los cambios a hacer en pesos y sesgos para el siguiente lote.

export default class BackPropagation {

...

    calculate(tunner: NetworkTunner) {
        const layerCount = this.network.layers.length;
        for (let layerIndex = layerCount - 1; layerIndex >= 0; layerIndex--) {
            const layer = this.network.layers[layerIndex];
            for (let nodeIndex = 0; nodeIndex < layer.length; nodeIndex++) {
                const node = layer[nodeIndex];
                this.calculateForNode(node, tunner);
            }
        }
    }

    private calculateForNode(node: Node, tunner: NetworkTunner) {

        if (node.layer == this.network.layers.length - 1) {
            const actualResult = node.activation;
            const expectedResult = this.expectedResult[node.index];
            this._totalCost += this.costFunction.calculate(actualResult, expectedResult);

            const costRespectActivation = this.costFunction.calculateFirstDerivative(node.activation, expectedResult);
            this.saveCostRespectActivation(node.layer, node.index, costRespectActivation);
        }

        const zRespectBias = 1;
        const activityRespectZ = this.network.activationFunction.calculateFirstDerivative(node.zValue);
        const costRespectActivation = this._costRespectActivationCache[node.layer][node.index];
        const costRespectBias = costRespectActivation * activityRespectZ * zRespectBias;
        tunner.addGradientComponentBias(node.layer, node.index, costRespectBias);

        for (let w = 0; w < node.weights.length; w++) {
            const zRespectWeight = this.network.calculateDerivativeOfInputRespectWeight(node.layer, node.index, w);
            const costRespectWeight = costRespectActivation * activityRespectZ * zRespectWeight;
            tunner.addGradientComponentWeight(node.layer, node.index, w, costRespectWeight);
            if (node.layer > 0) {
                const zRespectPreviousActivation = this.network.calculateDerivativeOfZRespectPrevActivation(node.layer, node.index, w);
                const costRespectPreviousActivation = costRespectActivation * activityRespectZ * zRespectPreviousActivation;
                this.saveCostRespectActivation(node.layer - 1, w, costRespectPreviousActivation);
            }
        }
    }

export default class NetworkTunner {

...

    addGradientComponentBias(layerIndex: number, nodeIndex: number, value: number) {
        this._gradient[layerIndex][nodeIndex].bias += value;
    }

    addGradientComponentWeight(layerIndex: number, nodeIndex: number, weightIndex: number, value: number) {
        this._gradient[layerIndex][nodeIndex].weights[weightIndex] += value;
    }

    apply(network: Network) {
        for (let i = 0; i < network.layers.length; i++) {
            const layer = network.layers[i];
            for (let j = 0; j < layer.length; j++) {
                const node = layer[j];
                const deltas = this._gradient[i][j];
                this.applyNodeChanges(node, deltas);
            }
        }
    }

    private applyNodeChanges(node: Node, gradientComponents: GradientComponents) {
        const biasDiff = gradientComponents.bias * this.learningRate.biasLearningRate;
        node.bias -= biasDiff;
        for (let w = 0; w < node.weights.length; w++) {
            const weightDiff = gradientComponents.weights[w] * this.learningRate.weightsLearningRate;
            node.weights[w] -= weightDiff;
        }
    }
}

La clase TrainEpochResult nos permite contabilizar el número de aciertos en cada época y la ganancia (cuánto disminuye el coste) entre una época y la siguiente:

export default class TrainEpochResult {

    duration: number = 0;
    cost: number = 0;
    costGain: number = 0;
    costGainPercent: number = 0;

    totalPredictions: number = 0;
    correctPredicitons: number = 0;

    constructor(readonly epochNumber: number) { }

    calculateGain(previousCost: number) {
        this.costGain = this.cost - previousCost;
        if (previousCost == 0) {
            return;
        }
        this.costGainPercent = Math.round(10000.0 * this.costGain / previousCost) / 100;
    }

    countResult(isCorrect: boolean) {
        this.totalPredictions++;
        if (isCorrect) {
            this.correctPredicitons++;
        }
    }

    get accuracy(): number { return Math.round(10000 * this.correctPredicitons / this.totalPredictions) / 100; }
}

La precisión de nuestra red será el porcentaje de aciertos respecto al total de intentos.

La salida del ejemplo será similar a esta:

$ ts-node ./src/main.ts

Epoch #0 total cost: 0.599452087801611 (0%). Accuracy: 0% 
Epoch #1 total cost: 0.5901566456523485 (-1.55%). Accuracy: 0% 

...

Epoch #8 total cost: 0.5478469500940051 (-0.79%). Accuracy: 50% 
Epoch #9 total cost: 0.5437631943013445 (-0.75%). Accuracy: 50% 

...

Epoch #31 total cost: 0.42510398809990124 (-1.85%). Accuracy: 100% 
Epoch #32 total cost: 0.41691815979552177 (-1.93%). Accuracy: 100% 

...

Epoch #999 total cost: 0.10974016776822586 (0%). Accuracy: 100% 

Training complete. Average accuracy: 98.05%

Si haces la prueba de ejecutar el script varias veces verás que unas veces aprenderá más rápido que otras, incluso en algunos casos terminará todas las épocas y no conseguirá una precisión mayor del 50%.

Prueba a cambiar el número de épocas, los rangos de los pesos y sesgos o el número de capas y nodos, y verás cómo cambian las capacidades de la red para aprender.

También te recomiendo que uses el depurador para seguir paso a paso cómo se calculan los valores durante el entrenamiento y entender así el funcionamiento interno.

6. Conclusiones

¡Pues esto es todo! si has comprendido todo hasta aquí puedes felicitarte, porque ya entiendes cómo funcionan y se entrenan las redes neuronales.

Espero que la lectura haya sido de provecho para entender un poco mejor este campo. He intentado pasar por encima de todos los conceptos necesarios, pero sin profundizar demasiado para que el contenido se pueda seguir con relativa facilidad.

Una de las ideas principales que me gustaría recalcar es que las Inteligencias Artificiales no son nada más que matemáticas. Conceptos bastante simples aplicados con ingenio para encontrar patrones en la realidad y para simular el comportamiento humano.

Y como matemáticas que son, cualquiera puede llegar a entender cómo funcionan.

7. Referencias

Te dejo algunas referencias que a mí me han resultado especialmente útiles para que profundices en el tema:

Vídeos

• Serie de dotCSV sobre redes neuronales.

• Serie de 3Blue1Brown sobre redes neuronales.

• Introducción a la IA Generativa de Google

Artículos

• Rockwell Anyoha:The History of Artificial Intelligence

• Jaime Durán: Todo lo que Necesitas Saber sobre el Descenso del Gradiente Aplicado a Redes Neuronales

• Stephen Wolfram: “What Is ChatGPT Doing … and Why Does It Work?”

• Douglas Reiser: “Building a Deep Neural Network from Scratch using TypeScript”

• Lunjia Hu: Backpropagation ≠ Chain Rule

• Sagar Sharma: Activation Functions in Neural Networks

• Jason Brownlee: How to Choose an Activation Function for Deep Learning

Libros

• S. Russell y P. Norvig: “Inteligencia Artificial, un enfoque moderno Si quieres profundizar en este campo, te recomiendo encarecidamente este libro donde encontrarás prácticamente todo lo que hay que saber sobre IA. Hay una nueva edición disponible.

• DeepLearning
• TypeScript